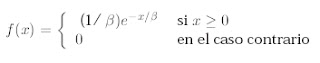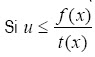GENERACIÓN DE VARIABLES ALEATORIAS

La generación de cualquier variable aleatoria se va a basar en la generación previa de una distribución uniforme (0,1). Y las transformaciones de dichos números generados en valores de otras distribuciones.

La mayoría de las técnicas utilizadas para la generación se pueden agrupar en:

Ø Método de la transformada inversa

Ø Método de aceptación-rechazo

Ø Método de composición

Ø Método de convolución

MÉTODO DE LA TRANSFORMADA INVERSA

Es el método más directo para generar una variable aleatoria. Sea

una función de distribución cuya función de distribución inversa es:

Sea U una variable aleatoria de   

se verifica que

tiene la función de distribución F. La prueba se sigue de la observación de que

Esto sugiere inmediatamente el siguiente esquema de generación:

Algoritmo del método de la transformada inversa

Propósito: Generar Z aleatoriamente de

Entrada: Capacidad para evaluar

Salida: Z

Método: Generar aleatoriamente U de

Devolver Z.

Ejemplo. La distribución exponencial

Supongamos que  tiene una distribución exponencial de media beta. La función densidad de probabilidad es:



La función de distribución (acumulativa) es:

MÉTODO DE ACEPTACIÓN RECHAZO

Este método es más probabilístico que el anterior. Los métodos de inversión, composición y convolución son métodos de generación directos, en el sentido en que tratan directamente con la función de distribución. El método de aceptación-rechazo es menos directo en su aproximación.

Se va aplicar este método en el caso de que la variable aleatoria sea continua, el caso discreto es análogo y está tratado en Prob. 8.9

En este caso tenemos la función de densidad f(x) de la variable y necesitamos una función t(x) que la acote, es decir t(x)³f(x) "x. Hay que notar que t(x) no es, en general, una función de densidad

pero la función r(x)=t(x)/c, si es claramente una función de densidad. (Suponemos que t es tal que c<¥). Debemos de poder generar (esperamos que de forma fácil y rápida) un valor de la variable aleatoria que sigue la función r(x). El algoritmo general queda como sigue:

Generar x que siga la distribución r(x)

Generar u~U(0,1), independiente de x



entonces devolver x si no volver a repetir el algoritmo

El algoritmo continúa repitiéndose hasta que se genera un valor que es aceptado.

Para hacer que se rechacen el menor número de puntos posibles la función t(x) debe ser la mínima función que acote a f(x).

MÉTODO DE COMPOSICIÓN

Este método va a poder ser aplicado cuando la función de densidad es fácil de

siendo n el número de trozos en los que se ha dividido la función.

Cada uno de los fragmentos se puede expresara como producto de un función de distribución y un peso

y la función de distribución global la podemos obtener como

El método consiste en generar dos números aleatorios, uno sirve para seleccionar un trozo y el otro se utiliza para generar un valor de una variable que sigue la distribución de dicho trozo. El valor de la variable obtenida es el valor buscado.

El algoritmo general queda como sigue:

Generar u1,u2~U(0,1)

Si u1=w1 entonces generar x~f1(x)

Si no

Si u1=w1+w2 entonces generar x~f2(x)

MÉTODO DE CONVOLUCIÓN

Muchas variables aleatorias incluyendo la normal, binomial, poisson, gamma, erlang, etc, se pueden expresar de forma exacta o aproximada mediante la suma lineal de otras variables aleatorias.

El método de convolución se puede usar siempre y cuando la variable aleatoria x se pueda expresar como una combinación lineal de k variables aleatorias:

En este método se necesita generar k números aleatorios (u1,u2,...,uk) para generar (x1,x2,...xk) variables aleatorias usando alguno de los métodos anteriores y así poder obtener un valor de la variable que se desea obtener por convolución.

REFERENCIAS BIBLIOGRAFICAS

• http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema5.pdf
• Coss Bu, Raúl; Simulación: un enfoque práctico; Editorial Limusa; 2003 
• http://jair.lab.fi.uva.es/~pablfue/leng_simulacion/materiales/func_alea_0405_resumen.pdf

descomponer en un conjunto de trozos,

NUMEROS ALEATORIOS: HISTORIA

NUMEROS ALEATORIOS

Los números aleatorios son aquellos que pueden ser generados a partir de fuentes de aleatoriedad, las cuales, generalmente, son de naturaleza física (dados, ruletas, mecanismos electrónicos o mecánicos), y son gobernados por las leyes del azar; éstos exhiben verdadera aleatoriedad en la realización de experimentos. Por su parte, los números pseudo-aleatorios son aquellas que tienen un comportamiento similar a la naturaleza aleatoria, pero están ceñidos a un patrón, generalmente de naturaleza matemática, que hace que su comportamiento sea determinístico.

HISTORIA DE LOS NUMEROS ALEATORIOS

Aproximadamente por le año 3500 a.C., juegos de azar con objetos de hueso, que podrian ser considerados como los precursores de los dados, fueron ampliamente desarrollados en Egipto y otros lugares. En el siglo XVII, un noble francés, Antoine Gombauld (1607-1684), puso en tela de juicio el fundamento matemático del éxito y fracaso en las mesas de juego. Formuló esta pregunta al matemático francés Balies Pascal (1623-1662): ¿Cuáles son las posibilidades de que me salgan dos seises por lo menos una vez en veinticuatro lanzamientos de un para de dados?, Pascal resolvió el problema, pues la teoría de la probabilidad empezaban a interesarle tanto como a Gombauld. Ambos compartieron sus ideas con el famoso matemático Pierre de Fernat (1601-1665), y las cartas escritas por los tres constituyen la primera revista académica dedicada a la probabilidad. Algunos de los problemas que ellos resolvieron habían permanecido si solución durante unos 300 años. Sin embargo, ciertas probabilidades numéricas para ciertas combinaciones de dados ya habían sido calculadas por Giordamo Cardano (1501-1576) y por Galileo Galileo (1564-1642)

Mas tarde, Jacob Benoulli (1654-1705), Abraham de Moivre (1667-1754), el reverendo Thomas Bayes (1702-1761) y Joseph Lagrange (1736-1813) inventaron formulas y técnicas de probabilidad. En el siglo XIX, Pierre Simón, marqués de Laplace (1749-1827), unifico esas primeras ideas y formuló la primera teoría general de la probabilidad, la cual fue aplicada inicialmente con buenos resultados a los juegos de azar; con el tiempo también se aplicó en la búsqueda de soluciones analíticas a problemas de naturaleza no deterministica. La teoría de la probabilidad ha sido constantemente desarrollada desde el siglo XVII y ampliamente aplicada en diversos campos de estudio. Hoy es una herramienta importante en la mayoría de las áreas de ingeniería,  ciencias y administración, y se constituye en la base para el estudio de las leyes de azar.

En cuanto a los números aleatorios, podemos afirmar que la historia formal de éstos  comenzó en la década de los cuarenta con el nacimiento del método llamado simulación de Montearlo, y Von Neumann, Metrópolis, Ulam y Lehmer pueden ser nombrados entre los pioneros en este campo. John Von Neumann aparentemente conjeturó el potencial de los computadores para tratar problemas estocásticos en 1945. Durante los cuarenta, la simulación de procesos estocásticos permaneció restringida al proyecto secreto del Departamento de Defensa de Estados Unidos. La publicación de The Monte Carlo Method por Metrópolis y Stanislaw M. Ulam en 1949 denota el inicio de la historia oficial del método. Dos años más tarde, D.H.Lehmer propuso el generador lineal de congruencia, el cual, con pequeñas modificaciones propuestas por Thomson y Rotenberg, ha llegado a convertirse en el método para la generación de números aleatorios mas ampliamente usado en la actualidad. Aunque originalmente el método de montecarlo fue implementado por John Von Neumann y Stanislaw Ulam, utilizando ruletas y dados en los problemas de difusión de los neutrones, en realidad su auge y creciente uso se debe a que hoy se emplean números aleatorios generados por computador.

Antes del advenimiento de las computadoras, los números aleatorios eran generados por dispositivos físicos. En 1939, Kendall y Babington-Smith publicaron 100000 dígitos aleatorios obtenidos con un disco giratorio iluminado con una lámpara relámpago. En 1955, la Rand Corporation publicó un millón de dígitos producidos controlando una fuente de pulsos de frecuencia aleatoria; estos se encuentran disponibles en cintas magnéticas de la Rand.

GENERACIÓN DE NÚMEROS ALEATORIOS

Una vez construido un modelo, debemos experimentar sobre él y para poder ejecutarlo necesitamos dar valores a las variables de tipo exógeno. De esta forma podremos obtener valores de salida y pasaremos a realizar un análisis de los mismos. Algunas de las variables de entrada son de tipo aleatorio por lo que se tendrán que generar valores que simulen dichas entradas. Para generar variables aleatorias que sigan determinadas funciones de probabilidad necesitamos partir de series de números que cumplan ciertas características de aleatoriedad. La generación de dichos números es lo que se va a abordar en este tema.

Método de congruencias aditivas.

Es un método rápido, puesto que no necesita realizar multiplicación. Se precisa una secuencia de números x1, x2. . . , xn. El generador produce una extensión de la secuencia xn+1, xn+2, . . . de la forma siguiente:

xi = (xi−1 + xi−n) mod m

Por definición a = b mod m si a−b es divisible por m (resto 0). Por ejemplo, en módulo 4, los números 2, 6, 10, 14 son equivalentes porque (10 − 2), (10 − 6) . . . son todos divisibles por 4. Hay que tener en cuenta que, cuando utilizamos módulo m, los valores que resultarán estarán comprendidos entre 0 y m-1.

Generadores de congruencias lineales

Una gran mayoría de los generadores utilizados actualmente utilizan esta técnica introducida por Lehmer en 1951. Una secuencia de números enteros Z1,Z2, . . . está definida por la fórmula recursiva:

Zi = (aZi−1 + c) mod m

donde el módulo m, el multiplicador a, el incremento c y la semilla o valor de comienzo

Z0 son enteros no negativos

Método de cuadrados medios: Fue  propuesto en la década de los 40 del siglo XX por Von Neumann y Metrópolis. Requiere un número entero detonador (llamado semilla) con D dígitos, el cual es elevado al cuadrado. Los pasos para generar números mediante cuadrados medios son:

1.       Seleccionar una semilla (X₀).

2.      Se eleva al cuadrado la semilla.

3.      Se extrae  la cantidad de dígitos del centro que se deseen, y este será X_1.

4.      Dividir X₁ entre 10000 y el resultado es el número aleatorio buscado.

5.      Repetir desde el paso 2 siendo la semilla X₁ hasta obtener la cantidad de número aleatorios deseados.

PROPIEDADES DE LOS NUMEROS ALEATORIOS

1. Uniformemente distribuidos: cualquier número que pertenezca al rango de interés debe tener la misma probabilidad de resultar sorteado.
2. Estadísticamente independientes (no correlación): tienen periodicidad cuando varios elementos, repetidos o no, formando una cadena, aparecen en la misma secuencia.
3. Periodo largo (sin repetición).
4. Reproducibles y mutables: cuando el Método comienza con la misma Semilla, debe dar la misma secuencia de números Pseudoaleatoreos.
5. Sencillo en su implementación.
6. Portabilidad.
7. Método rápido de generación: velocidad de generación acorde a las necesidades.
8. Poca memoria para la generación.

 REFERENCIA BIBLIOGRÁFICA

• Mancilla herrera Alfonso Manuel; numero aleatorios, Historia, teorías y aplicaciones, edición uninorte. 
• Sánchez Algarra, Pedro: Metodos estadísticos aplicados 

MAPA DE DISTRIBUCIÓN

SIMULACIÓN

La simulación es el desarrollo de un modelo lógico-matemático de un sistema, de tal forma que se obtiene una imitación de la operación de un proceso de la vida real o de un sistema a través del tiempo. Sea realizado a mano o en una computadora, la simulación involucra la generación de una historia artificial de un sistema; la observación de esta historia mediante la manipulación experimental, nos ayuda a inferir las características operacionales de tal sistema, citando dos pasos básicos de una simulación: a) desarrollo del modelo y b)  experimentación. El desarrollo del modelo incluye la construcción de ecuaciones lógicas representativas del sistema y la preparación de un programa computacional. Una vez que se ha validado el modelo del sistema, la segunda fase de un estudio de simulación entra en escena, experimentar con el modelo para determinar cómo responde el sistema a cambios en los niveles de algunas variables de entrada.

VENTAJAS Y DESVENTAJAS AL UTILIZAR LA SIMULACIÓN

VENTAJAS

1. Una vez construido, el modelo puede ser modificado de manera rápida con el fin de analizar diferentes políticas o escenarios.
2. Generalmente es más barato mejorar el sistema vía simulación, aquí hacerlo directamente en el sistema real.
3. Es mucho más sencillo comprender y visualizar los métodos de simulación que los métodos puramente analíticos.
4. Los métodos analíticos se desarrollan casi siempre, para sistemas relativamente sencillos donde suele hacerse un gran número de suposiciones o simplificaciones, mientras que con los modelos de simulación es posible analizar sistemas de mayor complejidad o con mayor detalle.
5. En algunos casos, la simulación es el único medio para lograr una solución.

DESVENTAJAS

1. Los modelos de simulación en una computadora son costosos y requieren mucho tiempo para desarrollarse y validarse.
2. Se requiere gran cantidad de corridas computacionales para encontrar "soluciones óptimas", lo cual repercute en altos costos.
3. Es difícil aceptar los modelos de simulación.
4. Los modelos de simulación no dan soluciones óptimas.
5. La solución de un modelo de simulación puede dar al analista un falso sentido de seguridad.